Projet GPS
Introduction Link to heading
Pour mon projet 3A à Centrale, j’ai dû trouver un sujet en rapport avec mon option de spécialisation à savoir les télécommuncations. Je me suis dit qu’il serait intéressant d’y rajouter une petite touche de cybersécurité pour rigoler un peu. J’avais à ma disposition un super outil qui s’appelle une HackRFOne. C’est un outil informatique qui permet d’envoyer des signaux radio de plein de fréquences et intensités différentes. C’est une radio-logicielle, c’est-à-dire qu’on peut modifier son comportement en la connectant à un ordinateur et en manipulant un logiciel. Nous verrons comment concrètement un peu plus loin.
En cherchant ce qui allait devenir un projet de plusieurs mois, j’ai découvert ce tutoriel qui m’a décidé à faire du sujet de GPS-spoofing, ou, pour franciser les choses : du leurrage GPS.
Sur cette page, je vais vous expliquer comment fonctionne le système GPS et comment on peut relativement facilement tromper certains récepteurs GPS en leur faisant croire qu’ils sont à des endroits autres que ceux où ils sont vraiment. C’est ce que nous appellerons tout au long de cette page, le leurrage GPS.
Introduction au GPS Link to heading
Le GPS (Global Positioning System) est, comme son nom l’indique, un système de géo-positionnement créé par les États-Unis à partir de 1973 et se termine en 1993. Le GPS fait partie d’un ensemble de GNSS (Global Navigation Satellite System) de plein de pays différents, on peut citer GLONASS pour la Russie qui débute en 1980 et se termine en 1996, le système chinois BeiDou démarré en 1993 qui a été complété en 2020, ainsi que le système européen Galileo, dont le premier lancé a eu lieu en 2005 et le dernier en 2024.
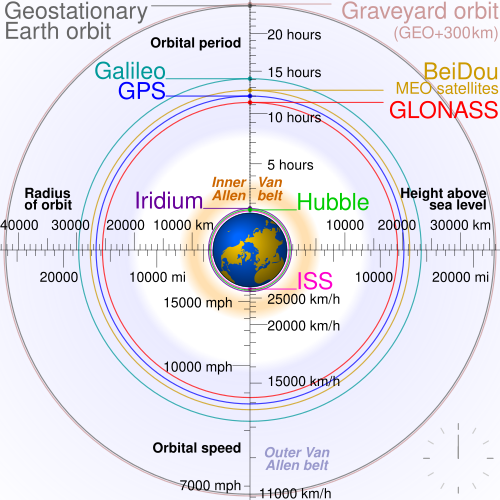
Remarquez l’orbite ‘cimetière’ pour les satellites décommissionnés
Il est bon de rappeler que tous ces projets s’inscrivent en réalité dans une continuité : il faut une maintenance permanente de la santé des satellites, prévoir des remplacements si besoin, des ajustements de courses pour maintenir un haut degré de précision avec des bases au sol pour effectuer des mesures étalons etc… De plus, avec les progrès technologiques, de nouveaux satellites avec de nouvelles fonctionnalités sont développés ce qui amène de nouveaux plans de déploiement. Pour chaque GNSS, on peut compter plusieurs générations de satellites, tous avec de nouvelles caractéristiques.
Les GNSS représentent évidemment des enjeux diplomatiques importants, au même titre que l’armement. C’est pourquoi différentes nations cherchent à développer leur propre technologie. On peut d’ailleurs noter que la plupart des systèmes GNSS ont une fréquence d’utilisation civile, et une fréquence chiffrée, souvent bien plus précise, pour une utilisation militaire. Beaucoup plus de choses pourraient être dites à ce sujet, mais laissons la géopolitique aux géopoliticiens, et revenons à un aspect plus technique !
Principe de fonctionnement Link to heading
Il faut minimum 3 satellites pour localiser un récepteur GPS dans l’espace (latitude, longitude, altitude) et un 4ème pour corriger les incertitudes de temps. C’est le travail du récepteur de faire sens de ces données et éventuellement les indiquer sur une carte interactive par exemple.
Calcul de position Link to heading
On veut trouver 3 inconnues, nos valeurs de latitude, longitude et altitude. Appelons-les $x, y, z$. On appellera $x_i, y_i, z_i$ la position du satellite $i$, ces valeurs-là ne sont pas inconnues car les satellites connaissent leur propre position dans le temps et communiquent ces informations dans leurs émissions.
Calcul de la distance au satellite Link to heading
Le récepteur est capable de calculer sa distance au satellite avec le calcul simple suivant :
$$ C = \frac{D}{\Delta t} \Rightarrow D = C*\Delta t $$- C est la vitesse de la lumière (connue)
- D est la distance au satellite (inconnue)
- Δt est la différence de temps entre l’émission du satellite et la réception du récepteur (que calcule le récepteur).
Voici un schéma explicatif, avec un smartphone en guise de récepteur. Le satellite émet un signal qui contient le temps très précis d’émission.
Fait avec Drawio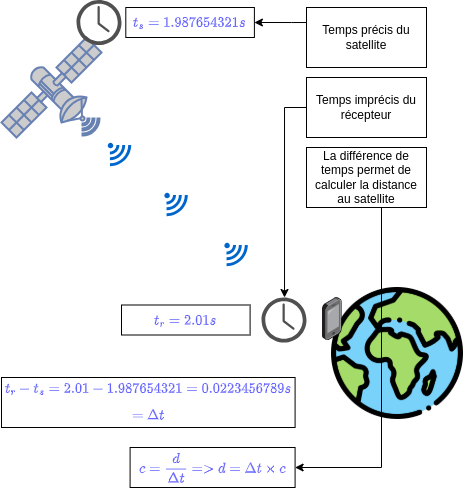
Maintenant qu’on a la distance $D_i$ au satellite $i$, on peut poser l’équation suivante :
$$ \sqrt{(x-x_i)² + (y-y_i)² +(z-z_i)²} = D_i $$On refait la même opération avec tous les trois satellites, et on obtient un système à 3 inconnues (toujours nos $x, y, z$) et 3 équations :
$$ \sqrt{(x-x_1)² + (y-y_1)² +(z-z_1)²} = D_1 $$$$ \sqrt{(x-x_2)² + (y-y_2)² +(z-z_2)²} = D_2 $$
$$ \sqrt{(x-x_3)² + (y-y_3)² +(z-z_3)²} = D_3 $$
On peut donc résoudre ces équations et obtenir nos valeurs pour $x, y, z$ et donc notre position. On note que puisque des puissances au carré sont impliquées, il va souvent y avoir deux points possibles en théorie, mais pas en pratique. Le chapitre suivant donne une intuition géométrique au raisonnement analytique que l’on vient de faire.
Trilatération Link to heading
Quand notre position P est à une distance Da d’un point A, on sait qu’on est sur une sphère de rayon Da et de centre A.
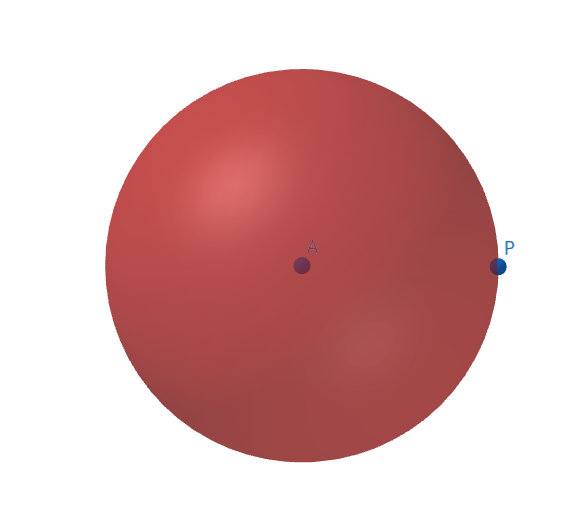
Fait avec GeoGebra
Si on rajoute une distance Db à un point B, l’intersection des deux sphères est un cercle.
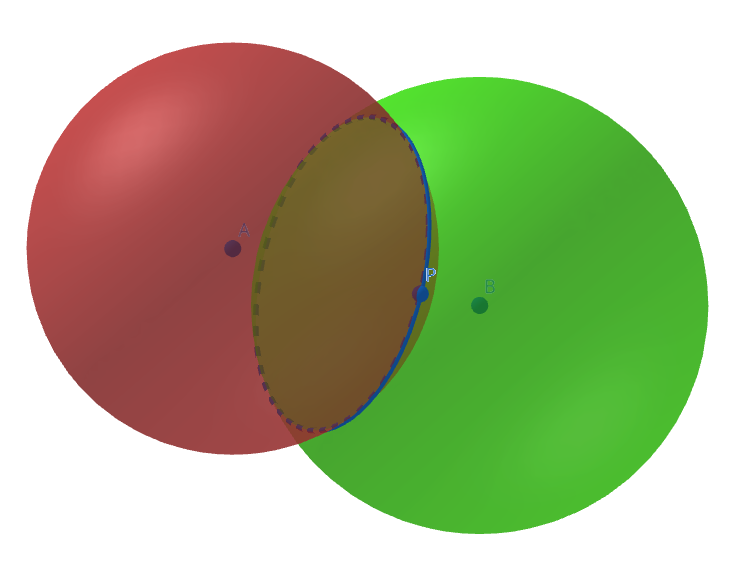
GeoGebra est notre ami
Si on rajoute encore une distance Dc à un point C, on obtient 3 sphères qui se coupent. Cela revient à 2 cercles qui se coupent, le plus souvent, en deux points, l’un des deux correspondant donc à notre localisation.
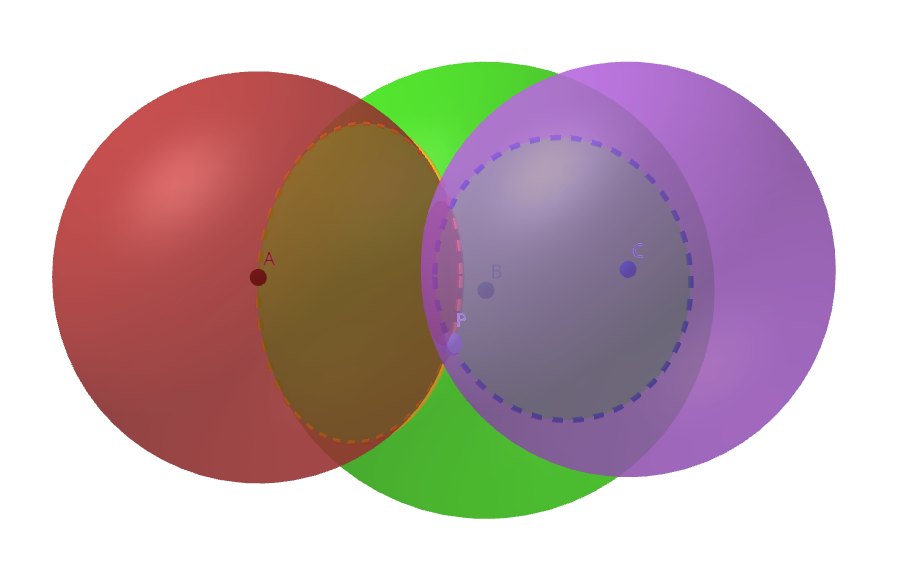
Gloire à GeoGebra
Mince, si seulement ça avait pu être un seul point au lieu de deux ! Mais rassurons-nous, en pratique, les récepteurs utilisent des méthodes de calcul numérique qui différencient automatiquement les deux, et de toute manière ils utilisent en moyenne aux alentours de 5 satellites rien que pour la position.
Correction des incertitudes temporelles Link to heading
⚠️ Attention ! ⚠️

Ce chapitre-là contient beaucoup de calculs, j’ai essayé du mieux possible de rendre ça lisible, mais la compréhension du détail de ces calculs n’est pas nécessaire. Vous pouvez tout aussi bien lire le résumé et passer à la conclusion.
Résumé : l’horloge du récepteur n’est pas aussi précise que l’horloge atomique du satellite, ce qui implique que la première est toujours en retard par rapport à la seconde. Quand le récepteur fait les calculs de la différence de temps entre l’émission et la réception du signal satellite, et ensuite de la distance entre le récepteur et le satellite, le retard fausse les calculs. Ce retard agit comme une 4ème inconnue (en plus de la latitude, longitude, altitude) et donc le récepteur trouve une 4ème équation pour la déterminer, avec, vous l’avez deviné, un 4ème satellite.
Vous aurez peut-être remarqué un problème lors du calcul de la distance précédemment. C’est que l’horloge de notre récepteur (disons un smartphone) est bien moins précise que les horloges atomiques à bord des satellites.
Qu’est-ce que ça implique ?
Eh bien prenons un exemple plus simple mais concret. Prenons une horloge peu précise qui compte seulement les secondes et qui affiche donc 1 s, et une horloge un peu plus précise qui compte aussi les dizaine de seconde et qui affiche donc 1,0 s. Voyons l’évolution de ces deux horloges sur 1 seconde entière sur le tableau suivant :
| Horloge peu précise | Horloge précise |
|---|---|
| 1 | 1.0 |
| 1 | 1.1 |
| 1 | 1.2 |
| 1 | 1.3 |
| … | … |
| 1 | 1.9 |
| 2 | 2.0 |
On voit que l’horloge peu précise a continué d’indiquer 1 alors que l’horloge précise indiquait des valeurs légèrement supérieures à 1. On constate donc que l’horloge peu précise à un retard systématique par rapport à l’horloge précise. Le graph de leur indication ressemblerait grossièrement à ça :
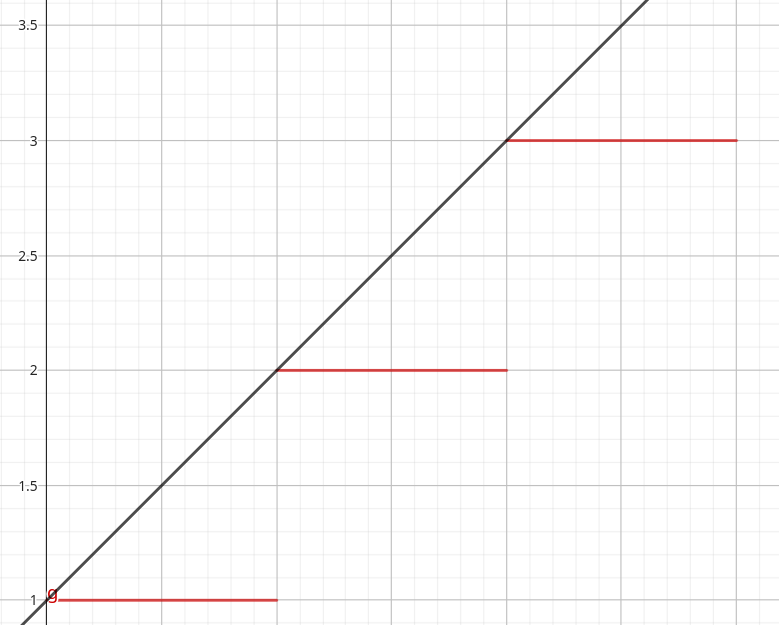
l’horloge précise en noir, la peu précise en rouge
Dans notre calcul, cela revient à dire que le temps du récepteur $t_r$ est toujours en retard par rapport au temps du satellite $t_s$. Pour compliquer les choses, ce retard n’est même pas constant dans le temps. Nous l’appellerons $\delta t^i$ à un instant $i$, tel que :
$$ \delta t^i = t_s^i - t_r^i $$Désolé pour toutes ces lettres de partout, je fais de mon mieux !!
Donc quand le récepteur calcule la différence de temps entre l’instant de réception (notée $^r$) du récepteur et l’instant d’émission (notée $^e$) du satellite :
$$ \Delta t = t_r^r - t_s^e $$Il le surestime ! On peut s’en convaincre avec les équations suivantes :
À l’instant d’émission, le retard nous donne :
$$ \delta t^e = t_s^e - t_r^e $$Soit :
$$ t_s^e = \delta t^e + t_r^e $$Donc :
$$ \Delta t = t_r^r - t_s^e = t_r^r - t_r^e - \delta t^e $$Par rapport à notre calcul de $\Delta t$ de tout à l’heure, on soustrait le terme $\delta t^e$, donc $\Delta t$ est en fait plus petit qu’on pensait, donc le récepteur le surestimait.
On s’accroche encore 2 minute !
Puisqu’on que le récepteur surestime $\Delta t$ et que $D = C \times \Delta t$, le récepteur surestime aussi la distance au satellite !
Par rapport à tout à l’heure, la distance est donc :
$$ D = C \times (\Delta t - \delta t^e)= C \times \Delta t - C \times \delta t^e $$Il faut donc indiquer à notre récepteur qu’il faut soustraire à la distance le terme : $C \times \delta t^e$.
Le problème c’est que notre récepteur, eh bien il n’a aucune idée de la valeur de $\delta t^e$, pour aucun des trois satellites nécessaires ! Donc comment obtenir cette valeur ?
Eh bien il la calcule avec un quatrième satellite !
Tout d’abord il suppose que tous les retards sont les mêmes pour chacun des trois satellites. Cette supposition va forcément impliquer des erreurs dans les calculs, mais elle permet malgré tout une bonne estimation.
Nos 3 équations à 3 inconnues de tout à l’heure se transforment en 4 équations à 4 inconnues grâce à un 4ème satellite :
$$ \sqrt{(x-x_1)² + (y-y_1)² +(z-z_1)²} - \delta t^e = D_1 $$$$ \sqrt{(x-x_2)² + (y-y_2)² +(z-z_2)²} - \delta t^e = D_2 $$
$$ \sqrt{(x-x_3)² + (y-y_3)² +(z-z_3)²} - \delta t^e = D_3 $$
$$ \sqrt{(x-x_4)² + (y-y_4)² +(z-z_4)²} - \delta t^e = D_4 $$
Et voilà le travail, la position est trouvée !
Conclusion Link to heading
Encore une fois, on pourrait rentrer dans des détails encore plus techniques, en parlant des effets relativistes qui doivent être pris en compte, de l’effet Doppler, des différences de phase, des interférences entre satellites, et certains aspects seront abordés plus tard mais beaucoup seront laissés de côté, premièrement pour un besoin de lisibilité et secondement car je suis moi-même loin d’avoir un tel niveau de compréhension.
Architecture d’un GNSS Link to heading
Les satellites Link to heading
Le GPS, comme tous les autres GNSS, a besoin de minimum 24 satellites actifs pour pouvoir correctement localiser un récepteur GPS sur Terre. Il en a actuellement 32 mais le nombre varie selon la retraite et le remplacement des anciens satellites par les nouveaux.
Il y a toujours au moins 4 satellites au-dessus d’un point donné
Les stations au sol Link to heading
Le système GPS dispose d’une douzaine de stations ou antennes au sol qui envoie régulièrement des informations aux satellites, typiquement des corrections de trajectoire. Puisque les stations savent ou elles se situent sur Terre, elles peuvent générer des éphémérides précises pour chaque satellite et leur communiquer.
Mon projet Link to heading
Principe de fonctionnement Link to heading
Si vous avez compris ce qui précède, vous devriez comprendre ce qui suit. Nous avons vu qu’il faut que 4 satellites envoient chacun leur éphéméride ainsi que le temps de leur émission ce à partir de quoi le récepteur peut calculer sa localisation précisément.
Cependant, toutes ces informations sont sous la forme d’ondes radio, et d’ondes radio de très faible intensité, puisque leur émetteur est littéralement dans l’espace, à environ 20000km de la surface de la Terre.
Donc en théorie, rien n’empêche de trouver les éphémérides de l’ensemble des satellites GPS en fonctionnement, de choisir des coordonnées sur la Terre, de calculer les signaux émis par les satellites que percevraient des récepteurs à ces coordonnées, d’en faire la somme et de les émettre à une intensité plus forte que les signaux authentiques.
Et c’est bien ça que vise à faire le tutoriel précédemment mentionné.
Choisir une localisation à leurrer Link to heading
La première étape est de choisir une localisation à leurrer. Choisissez n’importe où sur Terre, mais l’effet est plus impressionnant quand c’est très loin de là où on est actuellement. Au hasard, nous avons choisi un lac d’altitude en Argentine qui a les coordonnées suivantes :
-50.350396,-72.260449,100
Le 100 de la fin représente l’altitude, qui n’est pas spécialement importante puisque sur une interface telle que celle de Google Maps, on ne la perçoit pas. On la fixe à 100 par défaut pour un minimum de réalisme, mais c’est sans importance.
Récupérer les éphémérides Link to heading
La première étape du projet est de récupérer les éphémérides. Pour les satellites de la constellation GPS, c’est sans surprise la NASA qui s’en occupe. Elles sont mises à jour quotidiennement sur le site CDDIS, et on peut y accéder si on se crée un compte.
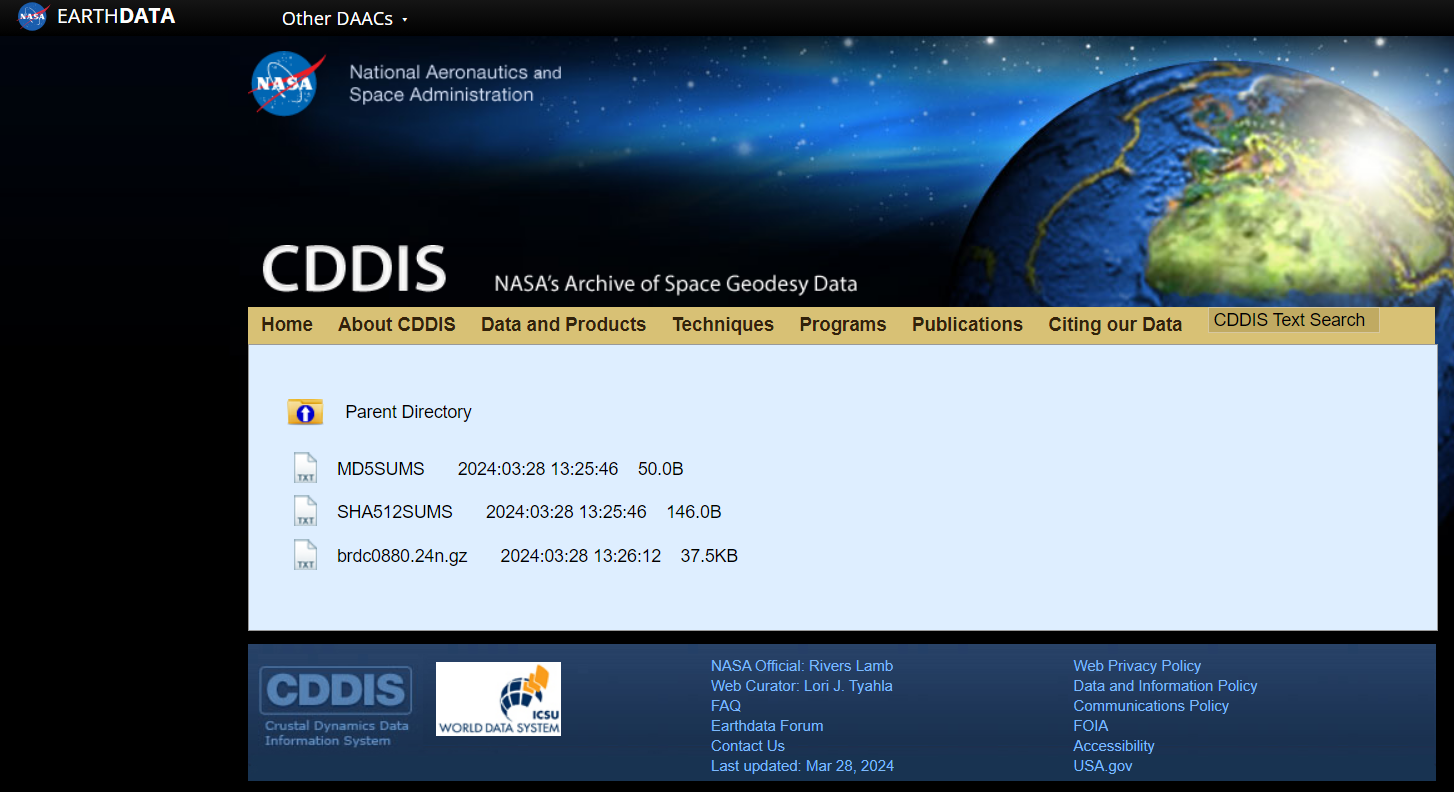
Le fichier brdc (court pour broadcast) est celui qui nous intéresse. Il finit par .gz car il est compressé. Téléchargeons-le dans notre dossier de projet.
Le calcul des signaux GPS Link to heading
Pour calculer les signaux pour chaque GPS, nous utiliserons l’outil gps-sdr-sim.
Une fois installé, la commande est simple :
gps-sdr-sim -e brdc3540.14n -l -50.350396,-72.260449,100 -o gpssim.bin
Ce qui en sort est un fichier binaire : gpssim.bin. C’est-à-dire illisible pour les humains, mais interprétable pour une SDR telle que la HackRFOne. Il s’agit de l’ensemble des signaux radios des satellites qui nous intéressent tous additionnés les uns aux autres.
Le leurrage Link to heading
Maintenant qu’on a le signal radio, tout ce qui nous reste à faire c’est d’émettre :
hackrf_transfer -t gpssim.bin -f 1575420000 -s 2600000 -x 0
hackrf_transfer est la commande qu’on invoque, à qui on donne comme paramètres le fichier gpssim.bin qui nous sort tout droit de l’étape précédente, la fréquence de 1575,420 MHz qui est la fréquence d’émission des satellites radio, une fréquence d’échantillonnage de 2,6 MHz pour le logiciel, et un gain de 0 (soit pas d’amplification en amplitude).
Et voilà le travail :
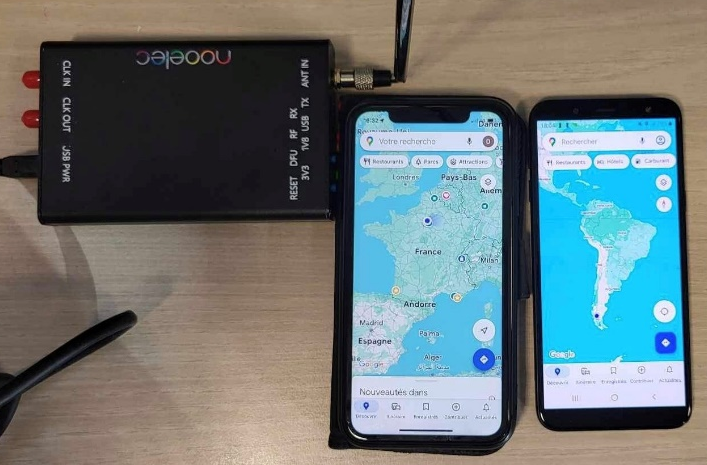
le téléphone de gauche qui se localise avec internet vs celui de droite avec le GPS, tous deux à côté de la HackRF en train d’émettre
Devinez lequel dit vrai et lequel se fait leurrer ! 😝
Les deux téléphones utilisent Google Maps pour se localiser, celui de gauche via internet et celui de droite via les signaux GPS, et on voit que les deux ne se localisent pas du tout au même endroit. J’étais évidemment à Paris à ce moment-là.
Leurrage dynamique Link to heading
Mais ça ne s’arrête pas là, maintenant qu’on peut leurrer une position fixe, pourquoi ne pourrait-on pas leurrer un ensemble de positions rapprochées au fil du temps pour donner une impression de mouvement ?
Eh bien c’est tout à fait possible et prévu par notre super outil : gps-sdr-sim !
Mais ça demande un peu plus de préparation.
Créer le trajet Link to heading
On va démarrer par dessiner notre trajet avec Google Earth. On met quelques points sur une carte pour dessiner la trajectoire qu’on veut simuler.
Création du fichier KML, convertit ensuite en CSV
En l’occurrence notre trajet sera une simple trajectoire rectiligne proche de la gare Saint-Charles. Je regrette maintenant de ne pas avoir une trajectoire un peu plus rigolote à vous montrer, mais je conseille fortement de faire plutôt une trajectoire cyclique et d’émettre en boucle ce qui sera sûrement plus amusant !
Voici à quoi ressemble le chemin :

On l’extrait dans le format KML, puis on va sur ce site pour le convertir en format CSV. On pourrait croire maintenant qu’il suffit de lancer la même commande avec le fichier CSV, mais en fait pas tout à fait.
Interpoler les positions Link to heading
En fait, dans le cas d’une émission dynamique, le logiciel gps-sdr-sim lit les données de position à 10Hz, c’est-à-dire 10 lignes par seconde. Sachant que par défaut le temps d’émission est 300 secondes, il faut donc au minimum 3000 lignes de fichier csv. S’il y a moins de lignes que ça sur notre fichier csv ce qui est très probable (on n’a mis que quelques points sur le trajet ci-dessus), on peut en rajouter en rajoutant des lignes (soit des positions) intermédiaires en utilisant des fonctions d’interpolation. C’est ce que fait le programme Python.
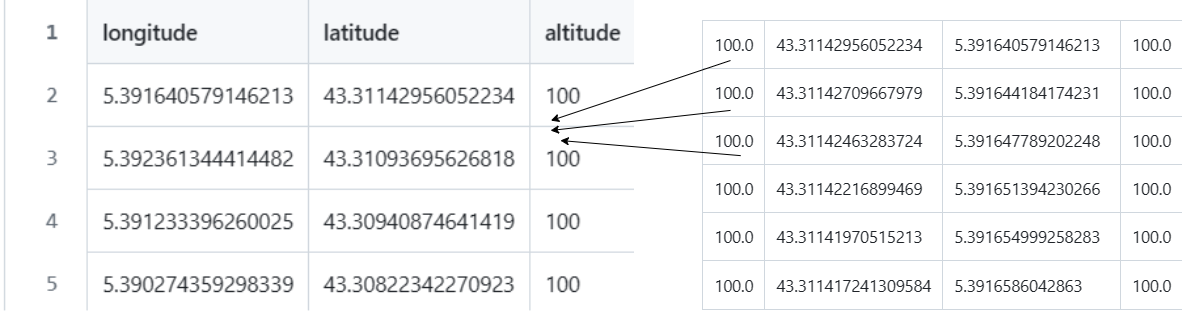
On rajoute des valeurs intermédiaires
Après ce traitement, on obtient un fichier csv d’une taille adéquate. C’est à partir de ce nouveau fichier qu’on crée notre fichier binaire :
gps-sdr-sim -e brdc3540.14n -x trajectoire.csv -o trajectoire.bin
Leurrons ! Link to heading
Tout est prêt désormais, il ne reste plus qu’à leurrer.
Lançons la commande :
hackrf_transfer -t trajectoire.bin -f 1575420000 -s 2600000 -x 0
On voit le point bleu bouger discrètement et la HackRFOne juste au-dessus
Si j’avais su qu’un jour je publierai ce projet sous forme de page web, j’aurais fait en sorte qu’on se rende mieux compte d’à quel point le point bleu bouge ! Malheureusement, je n’ai plus le matériel pour refaire l’expérience.
Et voilà, vous pouvez maintenant faire croire à vos amis qu’ils sont dans un train à l’arrivée de la gare Saint-Charles à Marseille ! Pratique non ?

Pauvre Lisa…
Comment se protéger du leurrage ? Link to heading
Avec ce qu’on vient de réaliser plus haut, on pourrait penser qu’il s’agit d’un gros problème d’ampleur internationale !
Heureusement, pas tout à fait.
Compétition avec les signaux légitimes Link to heading
Premièrement, les signaux GPS frauduleux sont en compétition avec les signaux GPS légitimes. Quand on est dans un bâtiment à plusieurs étages, souvent, ces signaux légitimes ne sont pas perçus par la plupart des récepteurs GPS et c’est pourquoi il est possible de les leurrer. Sans ça, souvent, ces récepteurs arrivent régulièrement à comprendre quels sont les bons signaux et auxquels faire confiance.
“Comment” me demanderiez vous ?
Je suis bien sûr encore loin d’être un expert mais de nombreuses variables peuvent entrer en jeu à mon sens :
- La puissance : les signaux GPS ont une amplitude très faible car ils viennent de loin, un signal frauduleux pourrait être bien plus puissant.
- La cohérence : si tout d’un coup le récepteur se met à percevoir une quinzaine de satellites en même temps (les faux et les vrais) selon sa programmation, il pourrait décider de se mettre en pause ou d’utiliser une autre méthode de localisation, ou de faire confiance à ceux qu’il perçoit depuis plus longtemps ou qui sont le plus cohérents avec sa dernière position enregistrée.
- La direction : si le récepteur est suffisamment bien construit, il pourrait avoir un module qui détecte de quelle direction viennent les signaux. S’ils semblent venir de l’espace, tout va bien, mais de la surface de la Terre, tout va mal !
Autres méthodes de localisation Link to heading
Un récepteur GPS pourrait en réalité être un récepteur multi-système, qui exploite les signaux de bien d’autres systèmes GNSS comme Galileo, BeiDou etc. Auquel cas, il serait tout à fait possible de programmer ce récepteur pour qu’il compare les positions données par les différents systèmes et qu’il ne fasse pas confiance à celui qui est trop loin des autres.
Sans compter sur les smartphones bien sûr pour qui l’utilisation des GNSS est même inexistante sur certains appareils, qui ne comptent que sur les antennes téléphoniques, 4G ou d’autres appareils proches pour se localiser (avec une précision effarante d’ailleurs).
Utilisation des signaux chiffrés Link to heading
Imaginez, vous avez toujours rêvé d’aller à Venise mais vous êtes dans un avion en direction de Tourcoing. Vous sortez votre HackRFOne et fort de vos connaissances fraîchement acquises en signaux GPS (de rien) vous commencez à leurrer dynamiquement l’avion pour qu’il change sa direction vers la ville de vos rêves.

Demi-tour, direction Venise
Malheureusement, ce scénario n’est pas vraiment plausible. D’une part car votre HackRFOne sera potentiellement saisie à la douane, et surtout parce que les avions utilisent bien entendu de nombreuses méthodes de navigation classique (un peu comme les marins à l’époque) mais aussi, je serais étonné s’ils utilisaient les signaux grand-public du GPS. Si vous vous souvenez de la présentation du système, vous savez que l’armée américaine n’utilise pas les mêmes signaux que nous, elle utilise des signaux chiffrés, protégés par mot de passe si l’on veut, qui sont bien plus précis.
Il me paraît raisonnable de supposer qu’il en est de même pour les avions militaires comme commerciaux.
Conclusion Link to heading
Ce projet aura été fort intéressant et m’aura appris bien des choses sur les protocoles radio, les SDR (telle que la HackRFOne), les systèmes de géo-localisation et l’implémentation de livrables informatiques.
J’ai même fait une démo en classe où de nombreuses personnes ont sorti leur smartphone (sous Android), ont coupé la 4G et ont constaté qu’il se faisait effectivement leurré leur position !
Sachez une chose, c’est que sur deux démos que j’ai présentées dans ma vie, toutes les deux ont fonctionné. J’en conclus donc que je suis immunisé contre l’effet démo, et qu’à l’avenir, mes démos marcheront systématiquement, pile comme je veux, dès la première tentative. C’est la seule conclusion logique non ?
Merci à tous de m’avoir lu et à bientôt !

La fin