GPS Project
Introduction Link to heading
For my 3rd-year project at Centrale, I had to find a topic related to my specialization: telecommunications. I thought it would be fun to throw in a dash of cybersecurity for good measure. I had access to a fantastic tool called a HackRFOne. It’s a piece of hardware that lets you send radio signals at a wide range of frequencies and intensities. It’s what’s called a software-defined radio (SDR), meaning you can change how it behaves by hooking it up to a computer and controlling it through software. We’ll see more concretely how that works later on.
While I was searching for what would become a months-long project, I stumbled upon this tutorial, which convinced me to go with the topic of GPS spoofing or, to put it in French: leurrage GPS.
On this page, I’ll walk you through how the GPS system works and how you can fairly easily trick certain GPS receivers into thinking they’re somewhere they’re not. That’s what we’ll be calling GPS spoofing throughout this write-up.
Introduction to GPS Link to heading
GPS (Global Positioning System), as the name suggests, is a positioning system created by the United States starting in 1973 and completed in 1993. GPS is part of a broader group of GNSS (Global Navigation Satellite Systems) from various countries. For instance, there’s GLONASS from Russia (1980–1996), China’s BeiDou (started in 1993 and completed in 2020), and Europe’s Galileo, which launched its first satellite in 2005 and its most recent in 2024.
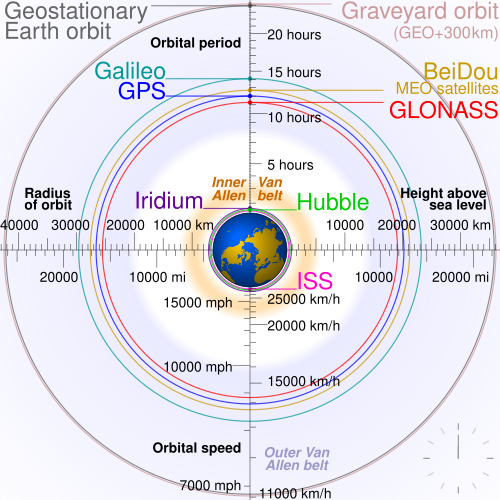
Note the ‘graveyard’ orbit for retired satellites
It’s worth noting that all of these systems require constant upkeep: satellite health monitoring, replacements when needed, orbit adjustments to maintain high precision, and ground stations for reference measurements. Plus, as technology improves, newer generations of satellites with updated capabilities are deployed, leading to continual development and upgrades.
GNSS systems are major geopolitical assets, much like weapons technology. That’s why many nations strive to develop their own systems. Most GNSS networks offer both a civilian signal and a separate encrypted (and usually more accurate) military signal. There’s a lot more to be said on this topic, but let’s leave geopolitics to the experts and get back to the tech!
How It Works Link to heading
You need at least 3 satellites to locate a GPS receiver in space (latitude, longitude, altitude), and a 4th to correct for time uncertainties. It’s the receiver’s job to make sense of the data and potentially display your location on an interactive map, for example.
Position Calculation Link to heading
We’re trying to find 3 unknowns: our latitude, longitude, and altitude. Let’s call them $x, y, z$. We’ll denote the position of satellite $i$ as $x_i, y_i, z_i$, these values aren’t unknown, because the satellites know their own positions in real time and broadcast that information.
Calculating Distance to a Satellite Link to heading
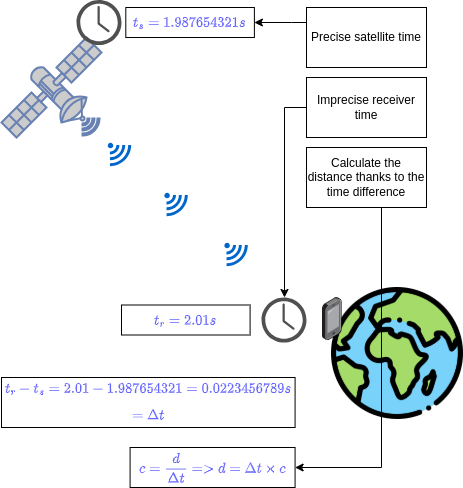
The receiver can calculate its distance to a satellite using this simple formula:
$$ C = \frac{D}{\Delta t} \Rightarrow D = C*\Delta t $$- C is the speed of light (a known constant),
- D is the distance to the satellite (unknown),
- Δt is the time difference between the signal’s emission by the satellite and its reception by the receiver (calculated by the receiver).
Here’s a diagram using a smartphone as a receiver. The satellite emits a signal that includes a very precise timestamp: Made with Drawio
Now that we have the distance $D_i$ to satellite $i$, we can write the following equation:
$$ \sqrt{(x-x_i)² + (y-y_i)² +(z-z_i)²} = D_i $$Repeating this for three satellites gives us a system of three equations with three unknowns ($x, y, z$):
$$ \sqrt{(x-x_1)² + (y-y_1)² +(z-z_1)²} = D_1 $$$$ \sqrt{(x-x_2)² + (y-y_2)² +(z-z_2)²} = D_2 $$
$$ \sqrt{(x-x_3)² + (y-y_3)² +(z-z_3)²} = D_3 $$
Solving this system gives us our position. Note that since squared terms are involved, there are often two possible solutions in theory, but only one makes sense in practice. The next chapter gives a geometric intuition behind this analytical reasoning.
Trilateration Link to heading
If your position P is at a distance Da from point A, then you know you’re somewhere on a sphere with radius Da and center A.
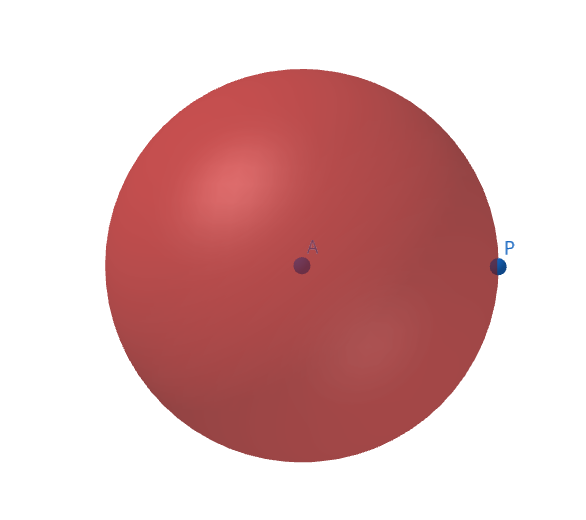
Made with GeoGebra
Add a second distance Db from point B, and the intersection of those two spheres is a circle.
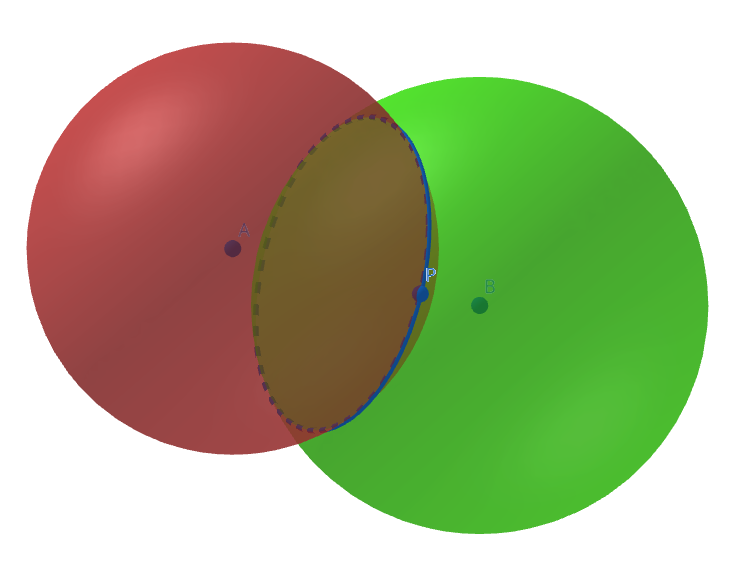
GeoGebra is our friend
Add a third distance Dc from point C, and you now have 3 intersecting spheres. This gives you two possible intersection points. Most often, only one makes sense and corresponds to your real location.
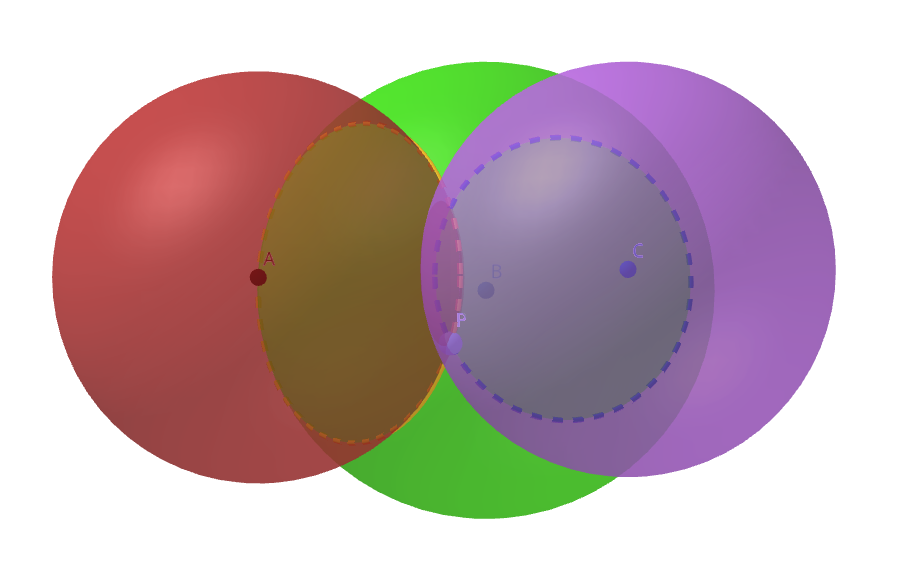
All hail GeoGebra
Too bad it’s not just a single point! But don’t worry. One of those two points is usually nonsensical, possibly located somewhere out in space, far from Earth. So the receiver can discard it and determine the correct location.
Correcting Time Uncertainties Link to heading
⚠️ Heads-up! ⚠️

This chapter has a lot of equations. I tried to keep it as readable as possible, but you don’t need to fully understand every detail. You can just read the summary and skip to the conclusion.
Summary: The receiver’s clock isn’t as precise as the atomic clocks on satellites, which means it’s always slightly behind. When the receiver calculates the time difference between emission and reception, and then uses that to compute distance, the delay throws off the result. This delay acts as a 4th unknown (in addition to latitude, longitude, and altitude). The receiver solves for it using, you guessed it, a 4th satellite.
You might have noticed a problem in the earlier distance calculation: our receiver’s clock (say, on a smartphone) is far less accurate than the atomic clocks onboard the satellites.
What does that mean?
Let’s take a simpler, concrete example. Imagine an imprecise clock that only counts in full seconds and shows 1 s, and a more precise clock that shows tenths of a second, so 1.0 s. Watch what happens over a full second:
| Imprecise Clock | Precise Clock |
|---|---|
| 1 | 1.0 |
| 1 | 1.1 |
| 1 | 1.2 |
| 1 | 1.3 |
| … | … |
| 1 | 1.9 |
| 2 | 2.0 |
You can see the imprecise clock lags behind the more precise one, displaying “1” even while the accurate one climbs. This means the imprecise clock is systematically behind. A graph of their outputs might look like this:
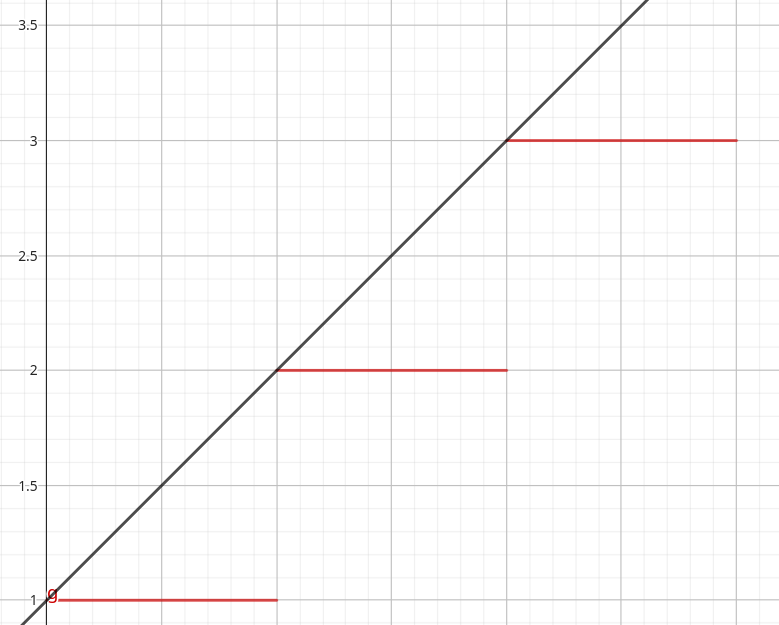
Precise clock in black, imprecise one in red
In our calculations, this means the receiver time $t_r$ always lags behind the satellite time $t_s$. To make it worse, this lag isn’t even constant over time. We’ll call it $\delta t^i$ at moment $i$, defined as:
$$ \delta t^i = t_s^i - t_r^i $$Sorry for the alphabet soup, I’m doing my best!
So when the receiver computes the time difference between the reception time (noted $^r$) and the emission time (noted $^e$):
$$ \Delta t = t_r^r - t_s^e $$…it ends up overestimating it! Let’s break it down:
At the moment of emission, the delay gives us:
$$ \delta t^e = t_s^e - t_r^e $$So:
$$ t_s^e = \delta t^e + t_r^e $$Therefore:
$$ \Delta t = t_r^r - t_s^e = t_r^r - t_r^e - \delta t^e $$Compared to our earlier $\Delta t$, we’re subtracting $\delta t^e$, which means the original estimate was too large. The receiver overestimated the signal’s travel time.
Almost there!
Since the receiver overestimates $\Delta t$ and $D=C\times\Delta t$, this means the receiver also overestimates the distance to the satellite.
So now, our corrected formula becomes:
$$ D = C \times (\Delta t - \delta t^e)= C \times \Delta t - C \times \delta t^e $$In other words, the receiver needs to subtract the term $C \times \delta t^e$ from its distance calculation.
But here’s the problem: the receiver has no idea what $\delta t^e$ actually is. Not for any of the three satellites! So how does it figure that out?
It uses a 4th satellite!
First, it assumes the delay is the same for all three satellites. This simplification introduces some error but still provides a decent estimate.
So our earlier system of 3 equations with 3 unknowns becomes 4 equations with 4 unknowns (adding $\delta t^e$):
$$ \sqrt{(x-x_1)² + (y-y_1)² +(z-z_1)²} - \delta t^e = D_1 $$$$ \sqrt{(x-x_2)² + (y-y_2)² +(z-z_2)²} - \delta t^e = D_2 $$
$$ \sqrt{(x-x_3)² + (y-y_3)² +(z-z_3)²} - \delta t^e = D_3 $$
$$ \sqrt{(x-x_4)² + (y-y_4)² +(z-z_4)²} - \delta t^e = D_4 $$
And there you go. Now we can solve for the position!
Conclusion Link to heading
Once again, we could go deeper into technical details: relativistic effects that must be accounted for, the Doppler effect, phase differences, satellite interference… Some of these will be covered later, but many will be left out. Partly for clarity, and also because, frankly, it extends far beyond my own understanding!
GNSS Architecture Link to heading
Satellites Link to heading
Like all GNSS systems, GPS needs at least 24 active satellites to ensure global coverage. Currently, there are 32, but this number changes with satellite retirements and replacements.
There are always at least 4 satellites above any given point
Ground Stations Link to heading
The GPS system has about a dozen ground stations that regularly send updates to the satellites. Mostly trajectory corrections. Since these stations know their exact positions, they can generate accurate ephemerides and send them to the satellites.
My Project Link to heading
How It Works Link to heading
If you understood what we covered so far, this next part should click. As we’ve seen, GPS receivers calculate position based on signals from 4 satellites, each transmitting its ephemerides and a timestamp.
But all that info is sent via radio waves. And very weak ones at that, since they’re coming from space, about 20,000 km above the Earth’s surface.
So, in theory, nothing stops us from grabbing the ephemerides for active GPS satellites, choosing coordinates anywhere on Earth, calculating what signals those satellites would emit to be received at those coordinates, summing them all up, and transmitting that signal at a higher power than the real ones.
And that’s exactly what the tutorial I linked earlier walks you through.
Picking a Location to Spoof Link to heading
The first step is picking a location to spoof. You can choose anywhere, but it’s more fun when it’s far from where you actually are. We randomly picked a high-altitude lake in Argentina with these coordinates:
-50.350396,-72.260449,100
The “100” at the end is the altitude in meters, not super important since mapping tools like Google Maps don’t really display it. We set it to 100 by default just for realism.
Getting the Ephemerides Link to heading
Step one: download the ephemerides. For GPS satellites, no surprise, it’s NASA that maintains them. They’re updated daily on CDDIS, and you can access them by creating an account.
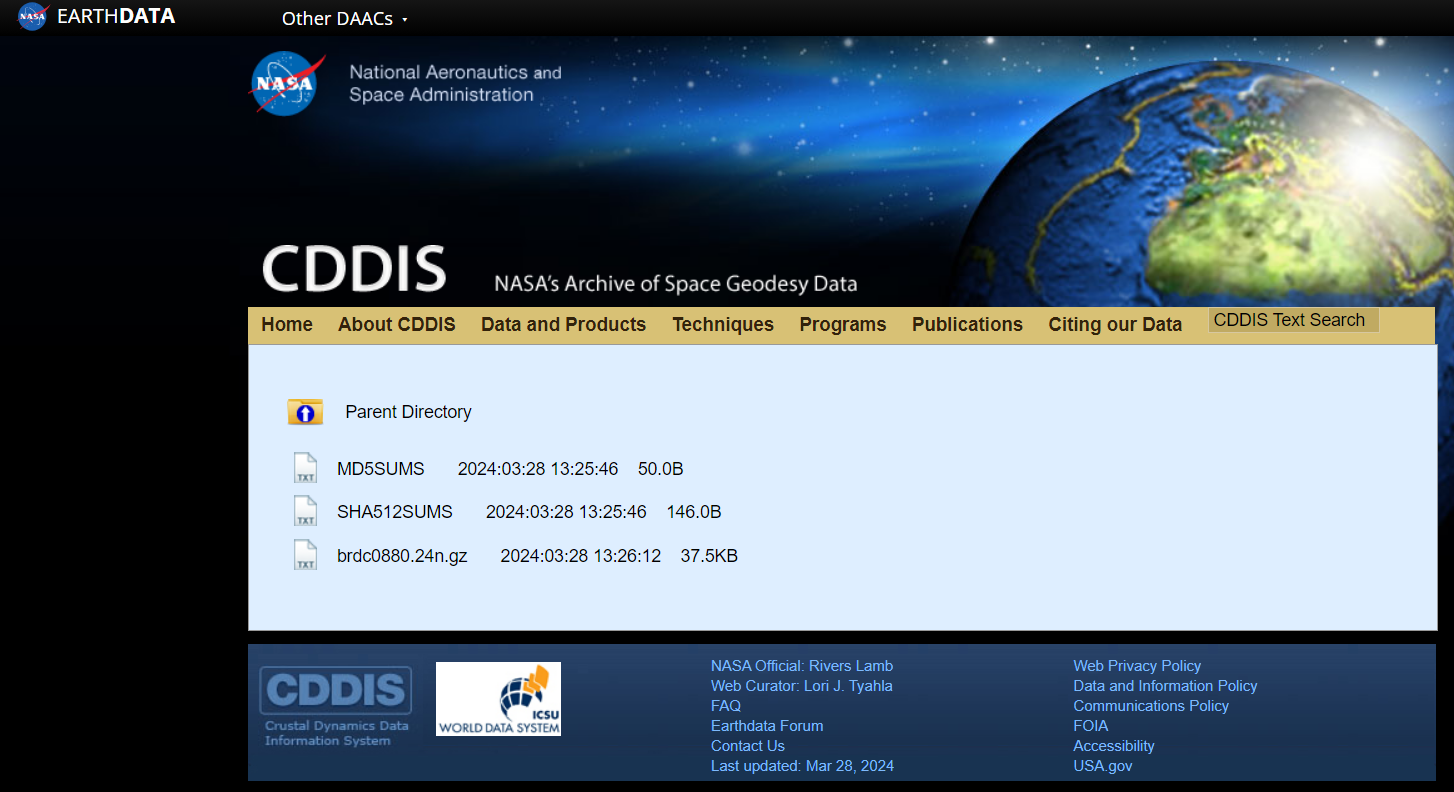
The brdc file (short for broadcast) is what we want. It ends in .gz because it’s compressed. Download it into your project folder.
Calculating the GPS Signals Link to heading
To calculate the signals from each GPS satellite, we’ll use gps-sdr-sim.
Once it’s installed, just run:
gps-sdr-sim -e brdc3540.14n -l -50.350396,-72.260449,100 -o gpssim.bin
This produces a binary file: gpssim.bin. Not human-readable, but perfect for an SDR like the HackRFOne. It’s the summed radio signals of the satellites relevant to our spoofed location.
The Spoofing Link to heading
Now that we’ve got our radio signal, all that’s left is to transmit it:
hackrf_transfer -t gpssim.bin -f 1575420000 -s 2600000 -x 0
Here’s what the command does:
-
-t gpssim.bin: our spoofed signal -
-f 1575420000: GPS broadcast frequency (1575.42 MHz) -
-s 2600000: sampling rate of 2.6 MHz -
-x 0: gain (0 = no amplification)
And voilà:
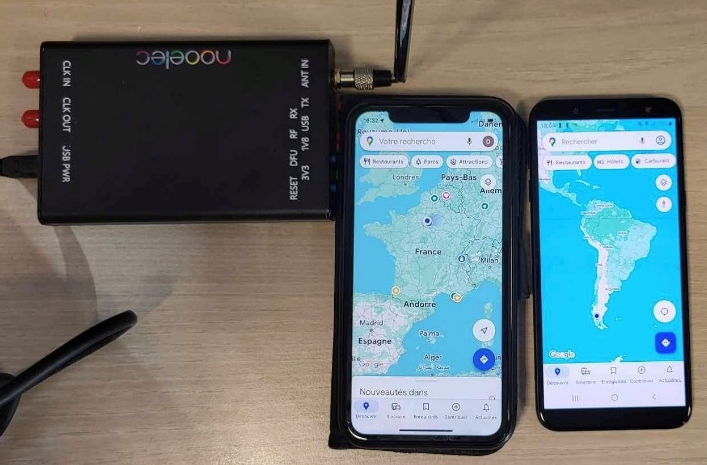
Left phone using internet vs right one using GPS, both next to the transmitting HackRF
Guess which one is being fooled! 😝
Both phones use Google Maps: one with internet, the other with GPS, and they show completely different locations. For the record, I was definitely in Paris when this happened.
Dynamic Spoofing Link to heading
But we’re not done yet! If we can spoof a fixed position, why not spoof a path, to simulate movement?
Well, that’s totally doable and supported by our trusty tool: gps-sdr-sim!
But it takes a bit more prep.
Drawing the Path Link to heading
First, we draw the path in Google Earth by placing waypoints to outline the trajectory we want to simulate.
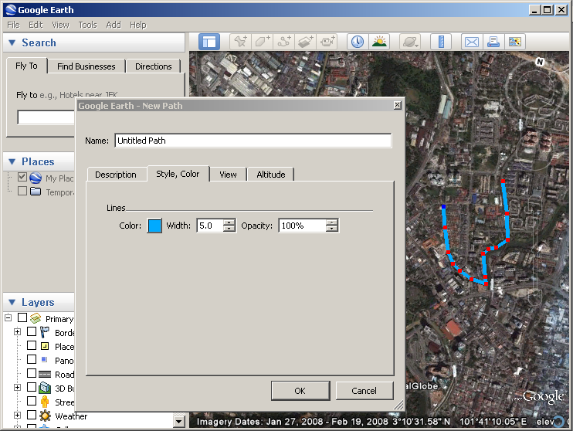
Creating the KML file, later converted to CSV
In this case, I made a simple straight line near Marseille’s Saint-Charles train station. In hindsight, I wish I’d made something more fun, like a looped path you can broadcast repeatedly!
Here’s what the path looks like:

Export it as a KML file, then use this site to convert it to CSV. But we’re not done just yet.
Interpolating Positions Link to heading
For dynamic spoofing, gps-sdr-sim expects location data at 10Hz, that means it reads and broadcasts 10 lines per second. Since the default duration is 300 seconds, we need at least 3000 lines in our CSV file. If your file has fewer (very likely if you only added a few waypoints), you’ll need to add intermediate positions using interpolation. That’s where a Python script comes in.
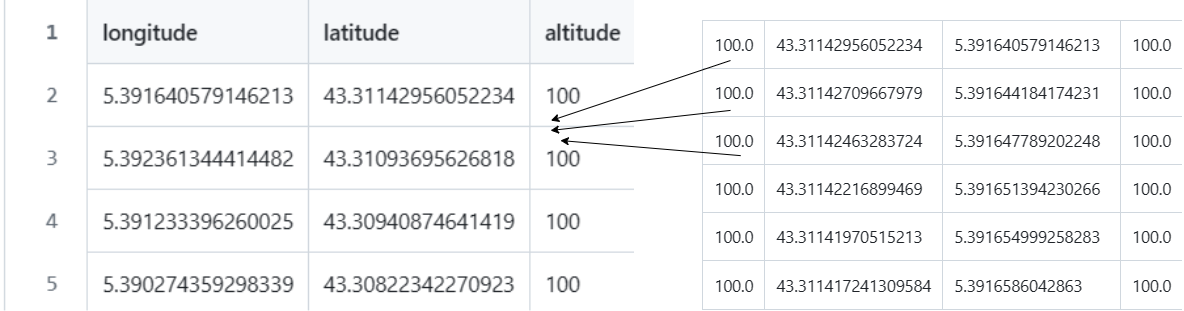
Adding intermediate values
Once that’s done, we have a CSV file with the required size. Now we can generate the binary file:
gps-sdr-sim -e brdc3540.14n -x trajectoire.csv -o trajectoire.bin
Spoof Away! Link to heading
Everything’s ready, let’s broadcast:
hackrf_transfer -t trajectoire.bin -f 1575420000 -s 2600000 -x 0
You can see the blue dot subtly moving, HackRFOne just above
If I had known I’d end up making a webpage out of this, I’d have made the movement easier to see! Sadly, I no longer have the equipment to redo it.
Now you can trick your friends into thinking they’re riding a train pulling into Saint-Charles station in Marseille. Handy, right?

Poor Lisa…
How Can You Protect Against Spoofing? Link to heading
After seeing how easy this seems, you might think it’s a massive global security flaw!
Luckily, not quite.
Competing with Legitimate Signals Link to heading
First, spoofed GPS signals are in direct competition with real ones. Inside multi-story buildings, legitimate signals are often weak or lost entirely, which is why spoofing works at all. Otherwise, receivers often manage to figure out which signals are real and ignore the rest.
“How?” you ask?
I’m no expert, but I imagine several factors play a role:
-
Power: Legit GPS signals are weak. A spoofed one might be suspiciously strong.
-
Consistency: If a receiver suddenly detects 15 satellites (both fake and real), depending on its software, it might pause, switch to another localization method, or prioritize the more consistent ones.
-
Direction: Advanced receivers could detect signal origin. Signals from space? Good. Signals from ground level? Suspicious.
Other Localization Methods Link to heading
A GPS receiver might actually be a multi-GNSS receiver, using Galileo, BeiDou, etc. It could be programmed to cross-reference signals and ignore any that are too far off.
And let’s not forget smartphones. Some don’t even rely on GNSS at all, but rather use cell towers, Wi-Fi, or other nearby devices (with surprising accuracy, by the way).
Use of Encrypted Signals Link to heading
Let’s say you’ve always dreamed of going to Venice but you’re on a plane to Tourcoing (a small french town perceived, mostly because of its name, as uninteresting). You whip out your HackRFOne and, using your fresh GPS knowledge (you’re welcome), start dynamically spoofing the plane’s location to Venice.

Turning around, heading to Venice
Sadly, not gonna happen. First, airport security might not love your HackRF. But more importantly, planes rely on many navigation systems (like old-school sailors), and I’d be very surprised if they used unencrypted public GPS signals. As we saw earlier, the U.S. military uses encrypted signals that are much more precise, and likely so do commercial aircraft.
Conclusion Link to heading
This project was fascinating and taught me a lot about radio protocols, SDRs (like the HackRFOne), geolocation systems, and how to implement real-world software tools.
I even did a live demo in class where many students (on Android phones) turned off their mobile data and saw their phones actually being spoofed!
And here’s one fun fact: of the two live demos I’ve ever given, both worked perfectly on the first try. So clearly, I’m immune to demo failures, and from now on, my demos will always succeed flawlessly. That’s the only logical conclusion, right?
Thanks so much for reading, and see you next time!

The End